In the previous article, we introduced the basic idea of neural networks and saw that an artificial neuron is a simplified version of the brain’s nerve cells. Now let’s take a closer look at how a biological neuron works and how we can model it in a computer.

How Does a Neuron Work?

The Biological Neuron

Without going into too much scientific detail, a biological neuron is made up of four main parts:

• Dendrites: it receives information from other neurons through these.
• Cell body (Soma): this processes the signals received by the dendrites.
• Axon: the neuron sends (or not) the processed signal through this.
• Axon terminals: the branches of the axon through which other neurons perceive the output signal.

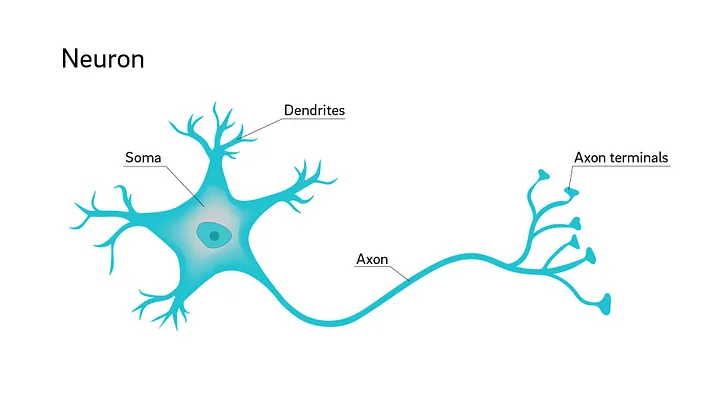
So, the cell body receives signals from other neurons through the dendrites, processes them, and if the signal resulting from the processing reaches a certain level, the neuron "fires", i.e. sends a signal through the axon to the other neurons connected to it.

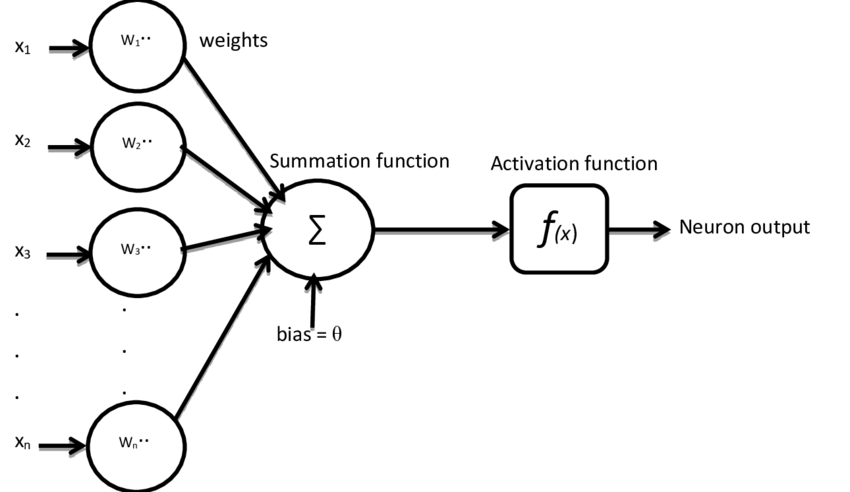
Artificial Neuron

The artificial neuron attempts to mimic this operation mathematically. Its most important parts are:

• Inputs: these simulate the dendrites, through which the neuron receives data.
• Weights: each input has a weight that shows how much the data arriving at the given input influences the output value.
• Bias: an offset is added to the weighted sum of the input signals, which can also influence the output result.
• Activation function: this makes the decision as to what value should be output by the neuron ("fire" or not) based on the previously summarized data.

In Mathematical Form

Let the inputs be in order x₁, x₂…x_n, their corresponding weights w₁, w₂…w_n, and the bias b. The operation performed by the neuron is as follows:

z=w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_n \cdot x_n + b

The activation function receives the value of z calculated in this way. In this case, let's take a simple step function that examines the input value and if it is zero or greater, it outputs 1, and if it is less than zero, it outputs 0.

y=\begin{cases} 1 & \text{ha } z \geq 0 \\ 0 & \text{ha } z < 0 \end{cases}

There are many types of activation functions (e.g. Sigmoid, ReLU, tanh), which we will discuss in a separate section later.

Python Example

Let's see how to program a neuron in Python:

# Bemenetek és súlyok
inputs = [0.5, 0.8]     # két bemenet
weights = [0.4, 0.7]    # hozzájuk tartozó súlyok
bias = -0.5             # eltolás

# Bemeneti értékek összegzése
sum = (inputs[0]*weights[0] + inputs[1]*weights[1] + bias) # 0.26

# Kimenet számítása a step függvénnyel
output = 1 if sum >= 0 else 0

print("A neuron kimenete:", output) # 1

# Inputs and weights
inputs = [0.5, 0.8]     # two inputs
weights = [0.4, 0.7]    # their associated weights
bias = -0.5             # bias

# Summarize input values
sum = (inputs[0]*weights[0] + inputs[1]*weights[1] + bias) # 0.26

# Calculating output with the step function
output = 1 if sum >= 0 else 0

print("Output of the neuron:", output) # 1

Next Article

In the next article, we will connect multiple neurons together and see how a simple layer is built. This will bring us closer to a complete neural network.