Az előző részben megismerkedtünk a neurális hálózatok alapgondolatával, és láttuk, hogy a mesterséges neuron az agy idegsejtjeinek egyszerűsített másolata. Most nézzük meg kicsit részletesebben, hogyan működik egy biológiai neuron, és hogyan modellezzük ezt a számítógépben.

Hogyan működik egy neuron?

Agyi neuron

Kerülve a tudományos alaposságot, az agyi neuron négy fő részből épül fel:

• Dendritek: ezeken keresztül kapja a többi neurontól az információkat.
• Sejtmag (Soma): ez dolgozza fel a dendritek által kapott jeleket.
• Axon: a neuron ezen keresztül küldi (vagy nem küldi) tovább a feldolgozott jelet.
• Axon végződések: az axon végének leágazásai, melyeken keresztül a többi neuron érzékeli a kimeneti jelet.

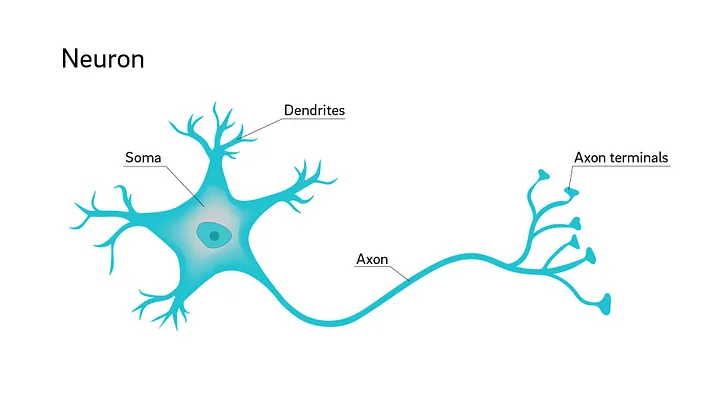
Tehát a sejtmag a dendriteken keresztül veszi a többi neurontól érkező jeleket, azokat feldolgozza és ha a feldolgozás eredményeként előálló jel elér egy bizonyos szintet, akkor a neuron „tüzel”, azaz az axonon keresztül jelet küld a többi, vele kapcsolatban lévő neuron felé.

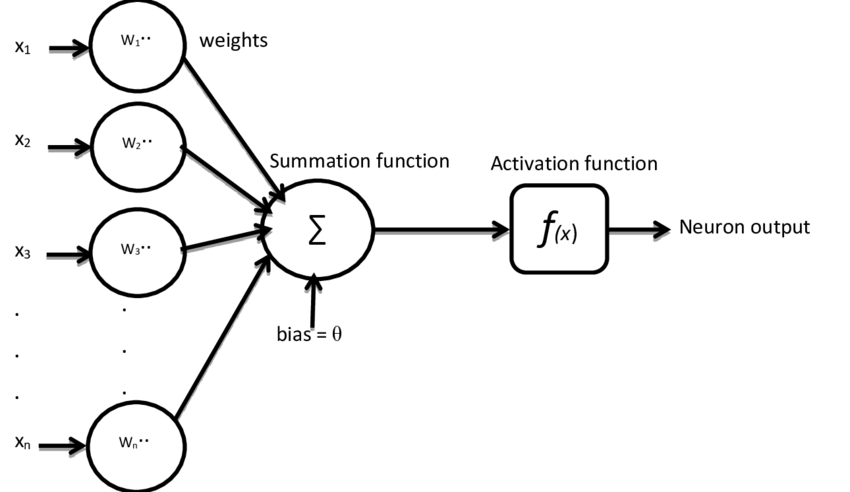
Mesterséges neuron

A mesterséges neuron ezt a működést próbálja utánozni matematikai úton. A legfontosabb részei:

• Bemenetek: ezek szimulálják a dendriteket, ezeken keresztül kapja a neuron az adatokat.
• Súlyok: minden bemenethez tartozik egy-egy súly, amely megmutatja, hogy az adott bemeneten érkező adat mekkora mértékben befolyásolja a kimeneti értéket.
• Eltolás (bias): a bemeneti jelek súlyozott összegéhez hozzáadódik egy eltolás, amellyel szintén befolyásolható a kimeneti eredmény.
• Aktivációs függvény: ez hozza meg a döntést, hogy a korábban összegzett adatok alapján milyen érték kerüljön a neuron kimenetére („tüzel” vagy nem).

Matematikai formában

Legyenek a bemenetek rendre x₁, x₂…x_n, a hozzájuk tartozó súlyok w₁, w₂…w_n, az eltolás pedig b. A neuron által elvégzett művelet a következő:

z=w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_n \cdot x_n + b

Az így kiszámolt z értéket kapja meg az aktivációs függvény. Jelen esetben vegyünk egy egyszerű step függvényt, ami megvizsgálja a beadott értéket és ha az nulla vagy annál nagyobb, akkor 1-et ad kimenetként, ha nullánál kisebb akkor pedig 0-t.

y=\begin{cases} 1 & \text{ha } z \geq 0 \\ 0 & \text{ha } z < 0 \end{cases}

Az aktivációs függvényeknek sok típusa van (például Sigmoid, ReLU, tanh), ezekről később egy külön részben fogunk beszélni.

Python példa

Nézzük meg, hogyan is programozzunk egy neuront Python nyelven:

# Bemenetek és súlyok
inputs = [0.5, 0.8]     # két bemenet
weights = [0.4, 0.7]    # hozzájuk tartozó súlyok
bias = -0.5             # eltolás

# Bemeneti értékek összegzése
sum = (inputs[0]*weights[0] + inputs[1]*weights[1] + bias) # 0.26

# Kimenet számítása a step függvénnyel
output = 1 if sum >= 0 else 0

print("A neuron kimenete:", output) # 1

# Bemenetek és súlyok
inputs = [0.5, 0.8]     # két bemenet
weights = [0.4, 0.7]    # hozzájuk tartozó súlyok
bias = -0.5             # eltolás

# Bemeneti értékek összegzése
sum = (inputs[0]*weights[0] + inputs[1]*weights[1] + bias) # 0.26

# Kimenet számítása a step függvénnyel
output = 1 if sum >= 0 else 0

print("A neuron kimenete:", output) # 1

Következő rész

A következő részben több neuront is összekapcsolunk, és megnézzük, hogyan épül fel egy egyszerű réteg. Ezzel már közelebb kerülünk egy teljes neurális hálóhoz.