A korábbi részekben felépítettünk egy réteget, amely kiszámolja a neuronok nyers kimenetét – vagyis a súlyozott bemenetek és a bias összegét. Ez a kimenet azonban lineáris: ha a bemenetet kétszerezzük, a kimenet is kétszeresére nő. Egy ilyen hálózat csupán egyenes vonalakat, azaz lineáris összefüggéseket képes megtanulni.
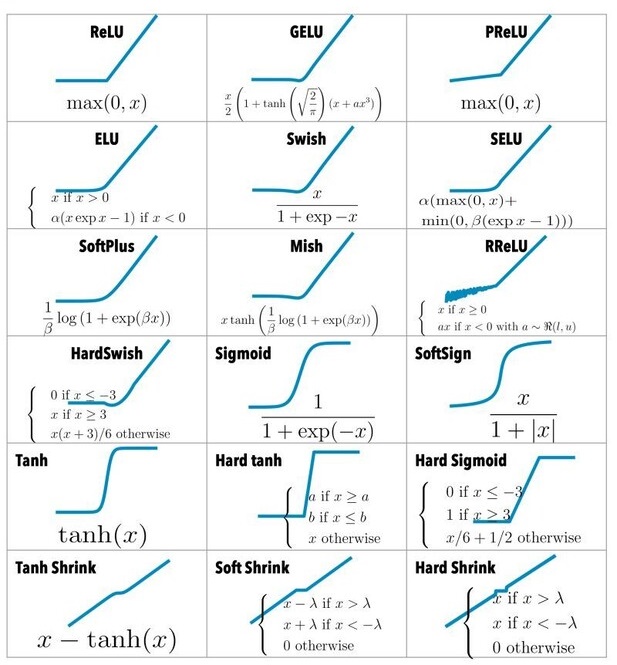
Csakhogy a világ nem lineáris. A képfelismerés, a beszédértés vagy a nyelvi feldolgozás mind olyan problémák, ahol bonyolult mintázatok jelennek meg. Ezeket egy tisztán lineáris modell sosem tudná megtanulni. Itt jönnek képbe az aktivációs függvények. Ezek azok a nemlineáris átalakítások, amelyek révén a neurális hálózat már nemcsak számol, hanem érzékelni és tanulni is képes mintázatokat.
Mi az aktivációs függvény szerepe?
Egy neuron kimenete aktiváció nélkül így néz ki:
output = sum (inputs * weights) + bias
Ha aktivációt is alkalmazunk:
output = f(sum (inputs * weights) + bias)
ahol f() az aktivációs függvény. Ez az apró, de kulcsfontosságú lépés adja meg a hálózat „intelligenciáját”.
Leggyakrabban használt aktivációs függvények
Step függvény
A legelső és legegyszerűbb aktivációs függvény a Step. A működése pofonegyszerű: ha a neuron bemenete egy adott küszöb felett van, a kimenet 1, ha alatta, akkor 0.
f(x) = \begin{cases} 1 & \text{ } x \geq 0 \\ 0 & \text{ } x < 0 \end{cases}Grafikusan ábrázolva:
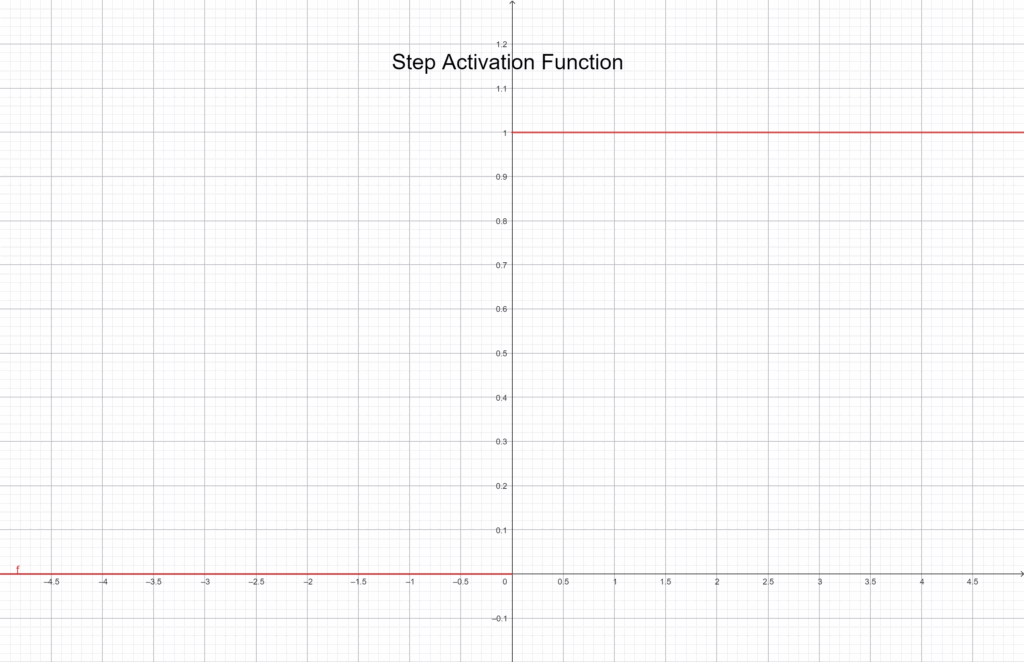
Ez a függvény jól szemlélteti, hogyan „kapcsol be” egy neuron, de tanításra nem alkalmas, mivel nem folytonos, és a gradiens-alapú tanulás (mint a backpropagation) itt nem működik. A Step függvény inkább tanítási célokra, demonstrációként hasznos – pont, ahogy mi is használtuk korábban.
Sigmoid függvény
A Sigmoid függvény már sokkal finomabb. Minden bemenetet 0 és 1 közé szorít, egy elegáns, S alakú görbe mentén:
f(x) = \frac {1} {(1 + e^{-x})}Grafikusan ábrázolva:
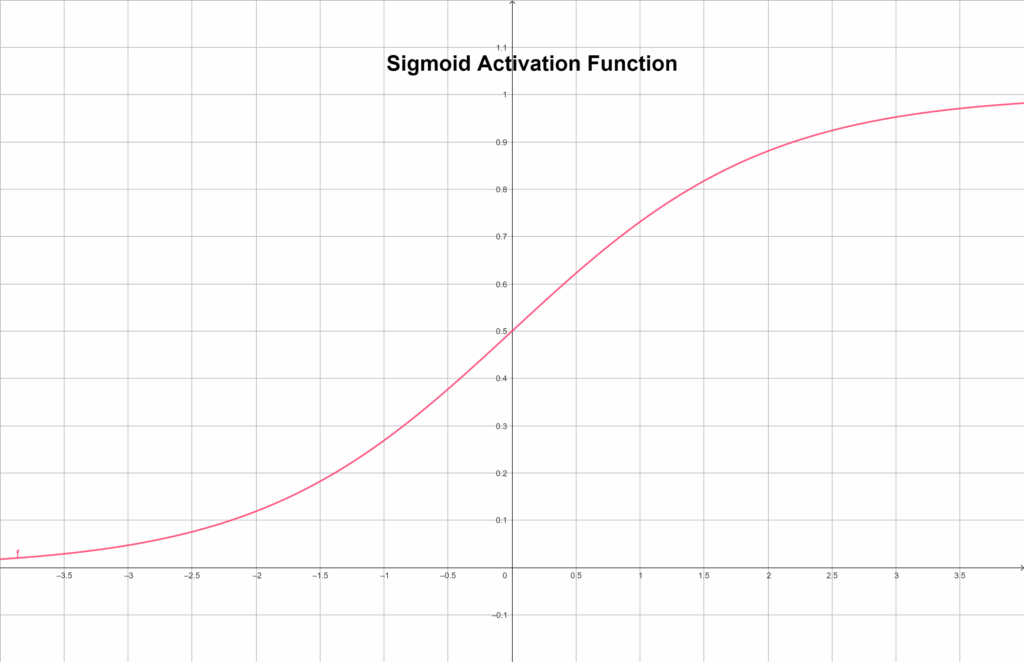
Ez azt jelenti, hogy a nagyon negatív értékek közel 0-t, a nagyon pozitívak közel 1-et adnak, a köztes tartományban pedig szépen fokozatosan nő az aktiváció. Emiatt jól használható ott, ahol valószínűséget akarunk becsülni – például bináris osztályozásban. Ugyanakkor a Sigmoid egyik gyenge pontja, hogy a szélső tartományokban a gradiens majdnem eltűnik, ezért a tanulás lelassulhat. Ezt hívjuk vanishing gradient problémának.
Tanh függvény
A tanh függvény, vagyis a hiperbolikus tangens, nagyon hasonlít a Sigmoidra, de a kimenetét -1 és 1 közé skálázza:
f(x) = tanh(x)
Grafikusan ábrázolva:
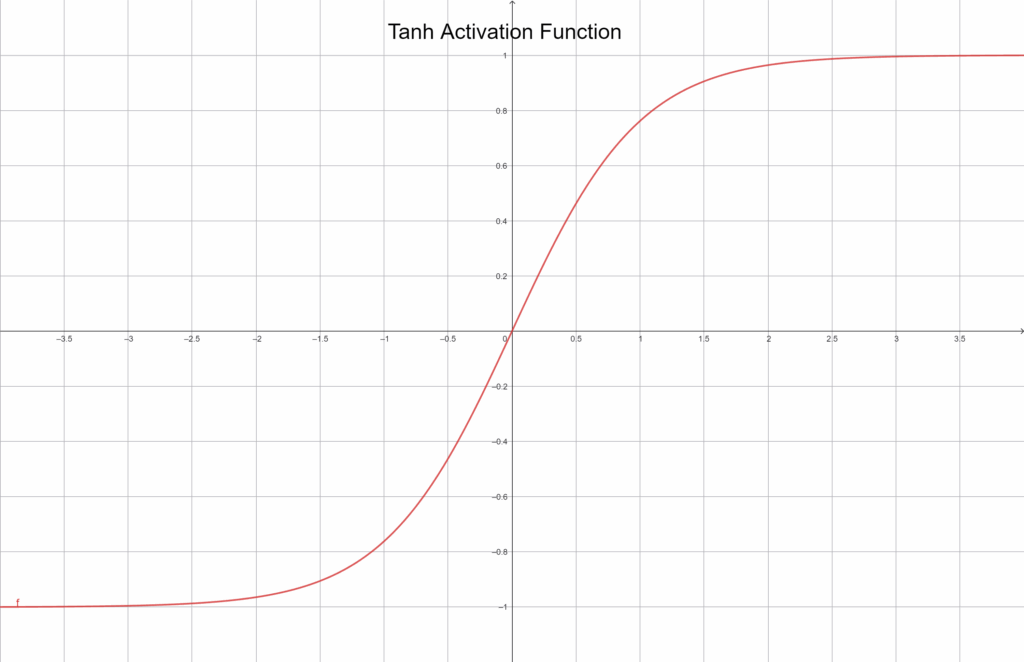
Ez a kis különbség sokat számít, mert a kimenet így a nulla körül ingadozik, ami gyakran gyorsabb és stabilabb tanulást eredményez. Ugyanakkor a Tanh sem tökéletes – a szélső értékeknél ugyanúgy el tud tűnni a gradiens. Mégis, sok régi és kisebb hálózatban ma is népszerű, mert intuitívan jól viselkedik és gyakran ad jobb eredményt, mint a Sigmoid.
ReLU (Rectified Linear Unit)
A ReLU talán a legismertebb és leggyakrabban használt aktivációs függvény a modern neurális hálózatokban. A működése nagyon egyszerű:
f(x) = max(0, x)
Grafikusan ábrázolva:
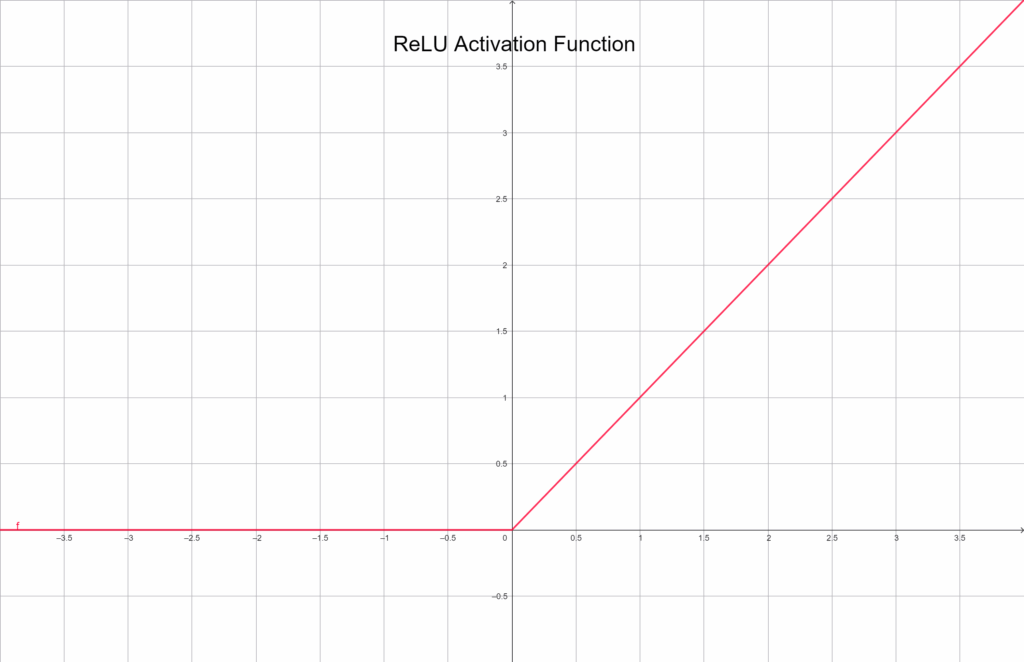
Ha a bemenet negatív, a kimenet 0. Ha pozitív, akkor az érték változatlanul továbbmegy. Ez a minimalizmus az ereje: gyors, egyszerű és segít elkerülni a Sigmoid-féle gradiensproblémákat. Ugyanakkor előfordulhat, hogy egy neuron negatív bemenetek miatt teljesen „meghal”, vagyis a továbbiakban sosem aktiválódik – ezt hívjuk dead neuron problémának. Mindezek ellenére a ReLU a legtöbb modern neurális hálózat alapértelmezett választása.
Leaky ReLU
A Leaky ReLU a ReLU továbbfejlesztett változata. A különbség csupán annyi, hogy a negatív tartományban sem nulláz le teljesen, hanem egy kis arányban tovább engedi az értéket:
f(x) = \begin{cases} x & \text{ } x \geq 0 \\ 0.01*x & \text{ }x < 0 \end{cases}Grafikusan ábrázolva:
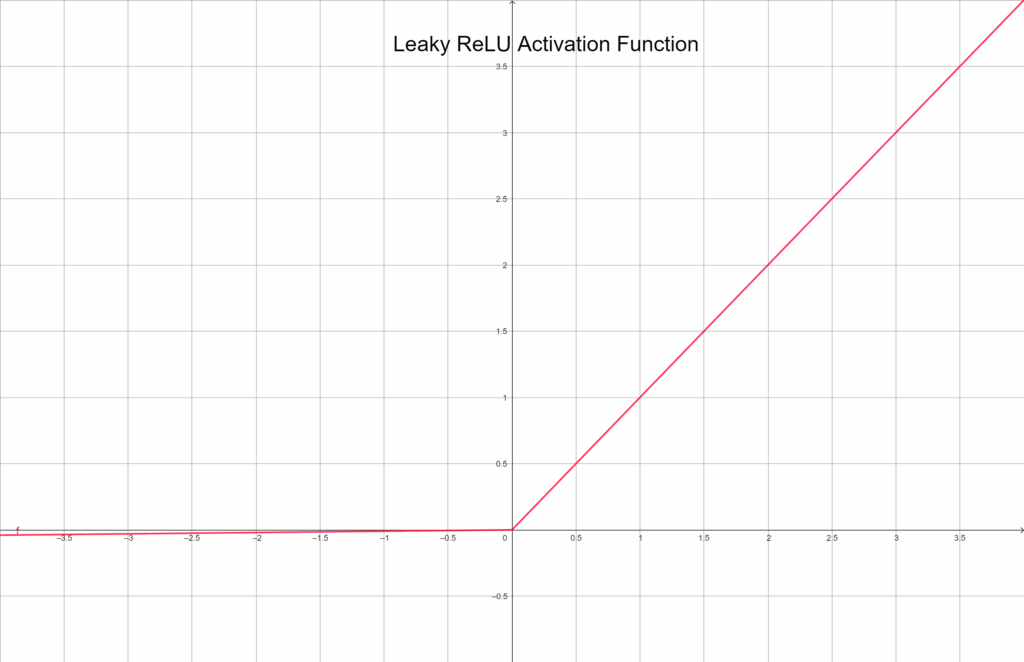
Ez a kis „szivárgás” életben tartja a neuront, még akkor is, ha sok negatív bemenetet kap. Emiatt stabilabb és kiegyensúlyozottabb lehet a tanulás. Gyakran használják ReLU helyett, ha a hálózatban túl sok neuron válik inaktívvá.
Összegzés
Az aktivációs függvények adják a hálózat nemlineáris erejét. Nélkülük a modell csupán egy lineáris összefüggést tudna leírni – ami nagyjából egy ferde sík vagy egyenes lenne. Az aktivációk azonban lehetővé teszik, hogy a neurális hálózat bonyolult, nemlineáris döntési határokat tanuljon meg, és ezáltal valóban intelligens viselkedést mutasson.
A következő részben megmutatjuk, hogyan valósíthatók meg ezek Pythonban és NumPy-val, és hogyan változtatják meg egy réteg működését a gyakorlatban.